All About EQ: Part 1

One of the most powerful tools at an audio tech’s disposal is EQ. But without a good understanding of what EQ does, your chances of using it successfully are pretty small. While at its core, EQ is a very simple form of audio processing, using it successfully takes some practice and knowledge. And used poorly, EQ can very quickly make a mix sound absolutely horrible.
So let’s start with the basics!
From Pitch to Frequency
Before we dive into EQ itself, let’s get some basic audio terminology established. While musicians refer to pitches by the names of the notes (A-flat, C-sharp, etc.), engineers (and many others) refer to pitches by their frequencies. Audio frequencies are measured in hertz (named for German physicist Heinrich Rudolf Hertz and abbreviated “Hz”) or kilohertz (for 1000 hertz and abbreviated “kHz”). Scientifically, the frequency is simply the number of complete cycles a given audio wave makes in one second as it moves through air. All sounds are, of course, made from vibration of one kind or another, and the faster the vibration, the faster the frequency, and the higher the pitch.
Music By Numbers
All notes in a musical scale have a particular numerical value, shown in the table below. You may notice that each octave halves (going down) or doubles (going up) the frequency of the same note in the previous octave. So the A above middle C is 440Hz (“A-440” is a commonly used pitch reference for tuning system), while the A above that is 880Hz and the one below is 220Hz. Convenient, right? All you have to remember is A-440 and that rule, and you’ll be able to get at least a numerical range for just about any set of notes.
Here is a table showing the cycles-per-second values in Hz for the notes of the musical scale grouped by octave.
| Oct | C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B |
| 0 | 16.35 | 17.32 | 18.35 | 19.45 | 20.6 | 21.83 | 23.12 | 24.5 | 25.96 | 27.5 | 29.14 | 30.87 |
| 1 | 32.7 | 34.65 | 36.71 | 38.89 | 41.2 | 43.65 | 46.25 | 49 | 51.91 | 55 | 58.27 | 61.74 |
| 2 | 65.41 | 69.3 | 73.42 | 77.78 | 82.41 | 87.31 | 92.5 | 98 | 103.8 | 110 | 116.5 | 123.5 |
| 3 | 130.8 | 138.6 | 146.8 | 155.6 | 164.8 | 174.6 | 185 | 196 | 207.7 | 220 | 233.1 | 246.9 |
| 4 | 261.6 | 277.2 | 293.7 | 311.1 | 329.6 | 349.2 | 370 | 392 | 415.3 | 440 | 466.2 | 493.9 |
| 5 | 523.3 | 554.4 | 587.3 | 622.3 | 659.3 | 698.5 | 740 | 784 | 830.6 | 880 | 932.3 | 987.8 |
| 6 | 1047 | 1109 | 1175 | 1245 | 1319 | 1397 | 1480 | 1568 | 1661 | 1760 | 1865 | 1976 |
| 7 | 2093 | 2217 | 2349 | 2489 | 2637 | 2794 | 2960 | 3136 | 3322 | 3520 | 3729 | 3951 |
| 8 | 4186 | 4435 | 4699 | 4978 | 5274 | 5588 | 5920 | 6272 | 6645 | 7040 | 7459 | 7902 |
A Look at the Waves
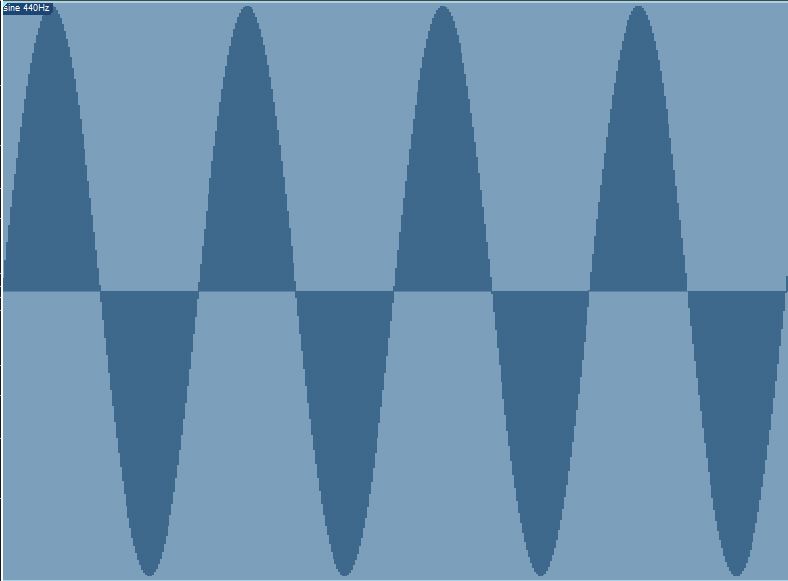
If you look at that A above middle C (so 440Hz) on an oscilloscope, digital audio workstation, or spectrum analyzer, you’ll see something like this:
This illustration shows four cycles of the audio wave. It starts at the center point, goes up to its maximum level on the positive side of the scale, goes back to the center, down to its maximum level on the negative side of the scale, and then starts the pattern over. With a frequency of 440Hz (so 440 cycles per second), you can determine that this illustration shows only 0.009 seconds (9 milliseconds) of time.
If you go up an octave to 880Hz, the wave will look like this:
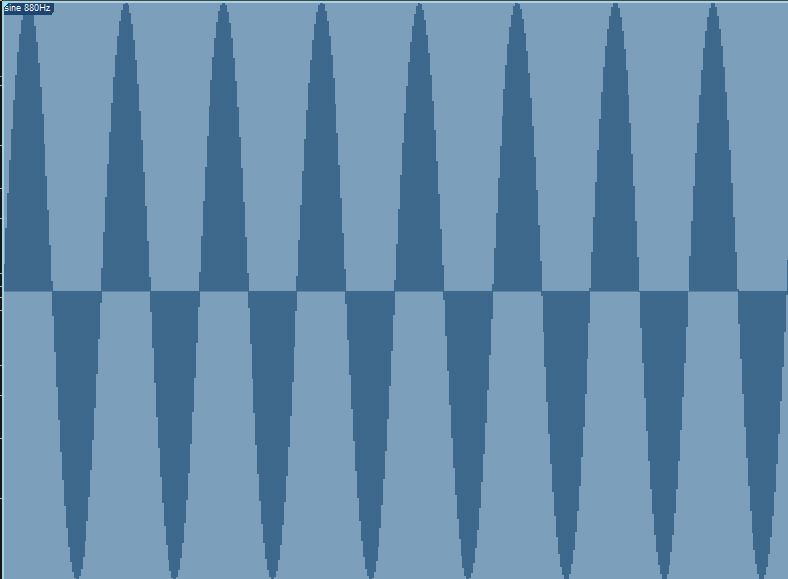
Doubling the frequency to 880Hz raises the pitch an octave and increases the number of cycles to 8 in the same time period.
In the same amount of time, the wave now completes twice as many cycles because the frequency is twice as fast.
Note that the height of the wave patterns—their amplitude–corresponds to the sound’s volume and has nothing to do with pitch or frequency. Thus, a quieter 440Hz tone would cross the center line at exactly the same points as the one shown above but would not extend as far above or below that center line. Same pitch but quieter—an essential point in considering EQ!
Beyond a Sine Wave
Now, if instead of using a tone generator to play your A-440, you walked up to a lovely Steinway concert grand piano and played an A above middle C, your sound wave image would look very different from the above example.
Why? Because the first example shows a sine wave produced by a tone generator or computer that is capable of producing only the frequency requested. That note on the piano has that frequency for sure, but it also has other frequencies mixed in as well. That main frequency (in this case, 440Hz) is called the fundamental, while the secondary frequencies are called harmonics (also sometimes called overtones). The tone generator has no harmonics, while the piano is full of them. Those harmonics are part of what give an instrument its characteristic tonality. Thus the piano version of A-440 will look like this:
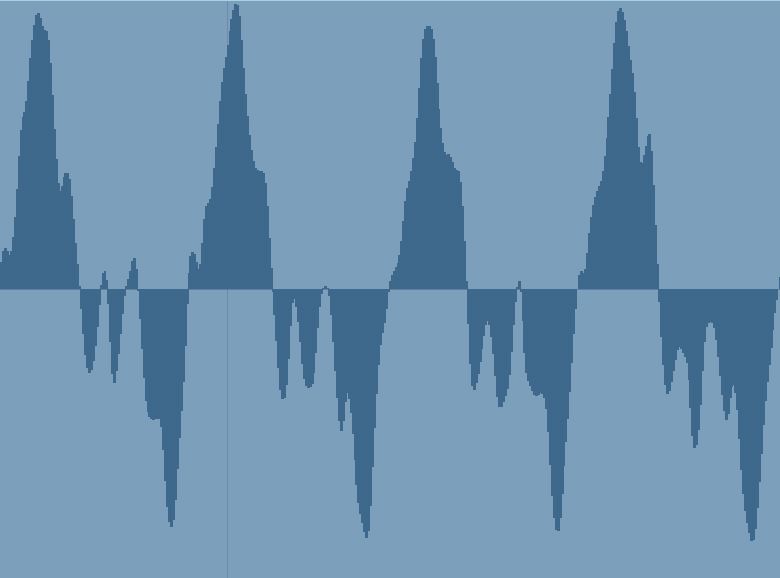
The same pitch played on a piano reveals the presence of harmonics in addition to the fundamental frequency of 440Hz.
In addition to harmonics, the piano sound will also have enharmonic tones which account for all the things that are the noises that make up the creation of the characteristic sound of the instrument—things like the hammer fall, damper noises, and so on. Without all the good enharmonic stuff, even a piano starts to sound like a sine wave organ. Same goes for guitar, drums, wind instruments, etc.
It’s essential to remember that different instruments have different numbers and types of secondary frequencies. And it’s also worth noting how the shape of the wave changes, even over just 9 milliseconds: the amplitude begins to drop immediately as the sound begins to decay after initial attack, and the decay is not uniform across all frequencies. This is particularly apparent when you extend the time window to 200 milliseconds (or two-tenths of a second):
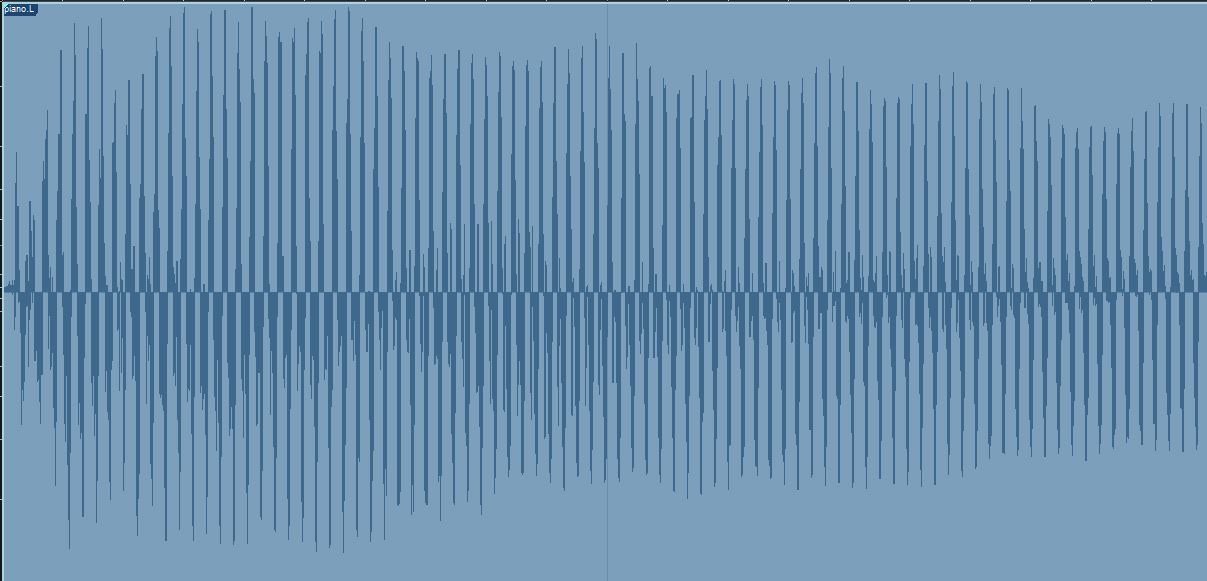
Extending the time window to 200 milliseconds reveals the complexity of the frequencies over the decay of the note.
With that cleared up, let’s switch over now to looking at the basics of EQ, beginning with what EQ really is.
Glorified Volume Control
EQ is short for equalization (or “equalisation” if you’re an Anglophile), and while it’s true that EQ changes the listener’s perception of the tone of most sounds, EQ is simply a specialized volume control. There’s no crazy complicated black-magic signal processing involved. It’s just a fancy volume control. So there’s nothing to be intimidated by; it’s just a fancy volume control.
Fun Fact: In the early days, EQ was intended to compensate for the deficiencies of early telephony equipment by applying filters to the audio signal to restore the balance between all the frequencies in the signal. That’s why it’s called equalizing.
What makes it fancy (and useful!) is that, unlike a standard volume control, EQ allows you to apply volume changes to only certain ranges of frequencies. And THAT translates to changes in tone. (Note: not all EQs work exactly the same, but they’re still all volume controls. What’s different about them is the ways they give you to control where the volume changes are applied. More on that in a future post in this series!)
Using Volume to Change Tone
So let’s go back to the first sine wave and the piano to look at what would happen if we applied EQ to those two signals. For the purposes of discussion, we’re going to use our EQ to boost frequencies in a 600-900Hz band.
On the 440Hz sine wave, what will happen? Right: nothing, because there are no frequencies in that signal in the frequency range that the EQ is working in. The EQ will boost frequencies between 600 and 900Hz the set amount, but that volume control is, in effect, trying to turn up silence. You’ll hear no difference between the pre- and post-EQ versions of the sine wave.
With the piano, however, it’s a very different story. The piano DOES have harmonics in that range, so boosting those frequencies will make those harmonic frequenciess louder. The fundamental (440Hz), as well as harmonics outside the 600-900Hz range specified by the EQ, will all be unaffected. This shifts the balance between all these different frequencies, which means certain harmonics are now louder than before. And how do we hear that? As a change in the tone of the piano, making it sound more brilliant than the pre-EQ version (or maybe harsher, if done too much).
Summary
So that’s the basics of how an EQ fundamentally works: by applying different volume changes (boosts or cuts) to different frequencies, an EQ alters the tone of a signal. In Part 2, we’ll look in more detail at more sound sources. Stay tuned!




1 Reply
Trackback • Comments RSS
Sites That Link to this Post